Trie data structure

I recently learned about a trie data structure. While it may not be as widespread as arrays, hash tables, linked lists, or binary trees, there are applications where it excels. The main advantage of a trie is that you can search in constant time, regardless of how many elements it contains. This makes tries useful for autocomplete systems, spell checkers, dictionaries, and similar applications.

A tree in black and white

Photo by David Bartus: https://www.pexels.com/photo/low-angle-view-of-lizard-on-tree-against-sky-320971/

Trie data structure

A trie grows like a tree, starting from a root node. Each node contains an array of its children and a boolean value to mark the end of a valid key. Otherwise, how would we distinguish keys with overlapping paths?

Consider a dictionary storing only one word: "apple". It consists of nodes a -> p -> p -> l -> e. Now, imagine that you wanted to search for the word "app". The program would go a -> p -> p, but at this point, there's no way to tell whether "app" is a valid word or just a part of "apple". This is where the boolean flag helps us.

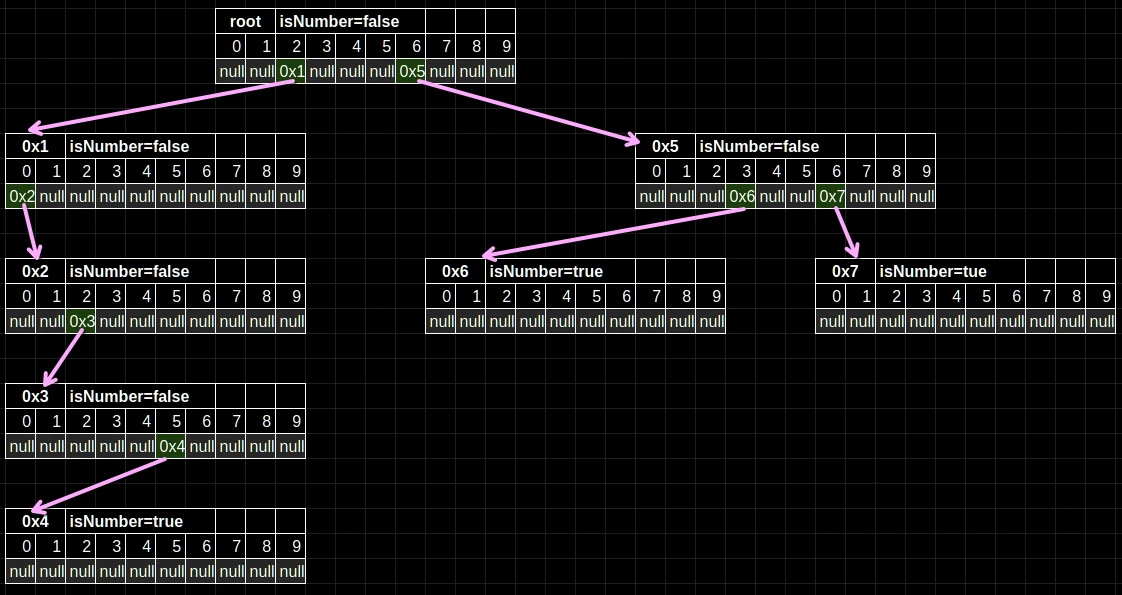
A picture is worth a thousand words. To keep it concise, I'll use numbers instead of strings as keys in the following example:

Trie data structure: visualized

Let us try to find "2025" by traversing it digit by digit.

Start at the root node. Is there a child for the digit "2"? There is! It points to another node at the arbitrary address of 0x1.
Go to 0x1. Is there a child node for "0"? Yes.
Go to 0x2. Is there a child node for "2"? Yes.
Go to 0x3. Is there a child node for "5"? Yes.
Go to 0x4.

By now, we've iterated over all digits in "2025". How can we confirm that "2025" is a valid key and not part of a bigger number, like in the example above with "apple" and "app"? We can check the isNumber property. For the node at 0x4 it is equal to true, so we know that "2025" is a legit key. We can also say that "202" isn't a valid key, because 0x3 tells us that isNumber is equal to false.

On the right side of the tree, we can also find "63" and "66". It doesn't matter whether the data structure contains those three elements or three billion elements, it will always take the same number of steps to find "2025", "63", and "66". How cool is that!?

Tries require arrays to store children of each node, which leads to higher memory consumption. However, the amount of time you save in certain cases makes them worthwhile. With hash maps, you'd rely on probing or chaining, which inevitably slows them down as more data is added.

Additional information

Here are two implementations that I found online:

https://www.geeksforgeeks.org/trie-data-structure-in-java/ - similar to my approach, but also covers additional use cases and runtime analysis
https://www.baeldung.com/trie-java - a different approach

I also want to emphasize that tries can store values, not just keys. In my examples, I focused on keys with spell-checking in mind. But you can replace isWord with any data type and use tries as a regular key-value storage.

Code

Below is my implementation in Java. Hopefully, it's correct 🔫

src/main/java/Dictionary.java

import java.util.Scanner;

import static java.lang.Character.toLowerCase;

public class TrieDictionary {
    private final Node root = new Node();

    public TrieDictionary(String filename) {
        load(filename);
    }

    private void load(String filename) {
        var file = getClass().getClassLoader().getResourceAsStream(filename);
        if (file == null) {
            throw new RuntimeException("dictionary not found");
        }

        try (var scanner = new Scanner(file)) {
            while (scanner.hasNextLine()) {
                insert(root, scanner.nextLine(), 0);
            }
        }
    }

    private void insert(Node node, String word, int n) {
        var i = toLowerCase(word.charAt(n)) - 'a';

        if (node.getChildren()[i] == null) {
            node.getChildren()[i] = new Node();
        }

        if (++n == word.length()) {
            node.getChildren()[i].setWord(true);
            return;
        }

        insert(node.getChildren()[i], word, n);
    }

    public boolean exists(String word) {
        return exists(root, word, 0);
    }

    private boolean exists(Node node, String word, int n) {
        var i = toLowerCase(word.charAt(n)) - 'a';

        if (node.getChildren()[i] == null) {
            return false;
        }

        if (++n == word.length()) {
            return node.getChildren()[i].isWord();
        }

        return exists(node.getChildren()[i], word, n);
    }
}

src/main/java/Trie.java

public class Node {
    private static final int EN_ALPHABET_LETTERS = 26;

    private boolean isWord = false;
    private final Node[] children = new Node[EN_ALPHABET_LETTERS];

    public boolean isWord() {
        return isWord;
    }

    public void setWord(boolean word) {
        isWord = word;
    }

    public Node[] getChildren() {
        return children;
    }
}

src/test/java/DictionaryTest.java

import org.testng.annotations.BeforeClass;
import org.testng.annotations.Test;
import org.testng.internal.collections.Pair;

import java.util.List;
import java.util.stream.Stream;

import static org.testng.Assert.*;

public class TrieDictionaryTest {
    private TrieDictionary trieDictionary;

    @BeforeClass
    public void setUp() {
        trieDictionary = new TrieDictionary("words_small.txt");
    }

    @Test
    public void textWithoutMisspelledWords() {
        var text = "How I Met Your Mother is an American sitcom created by Craig Thomas and Carter Bays for CBS".split(" ");

        for (String word : text) {
            assertTrue(trieDictionary.exists(word));
        }
    }

    @Test
    public void textWithMisspelledWords() {
        var text = "How I Meet Your Mother is an American sitcom cretaed by Craig Thomas and Carter Beys for CBS".split(" ");

        var expectedWords = List.of("Meet", "cretaed", "Beys");

        var actualWords = Stream.of(text)
                .map(word -> Pair.of(word, trieDictionary.exists(word)))
                .filter(pair -> !pair.second())
                .map(Pair::first)
                .toList();

        assertEquals(actualWords.size(), expectedWords.size());
        assertTrue(actualWords.containsAll(expectedWords));
    }

    @Test
    public void partialWords() {
        assertTrue(trieDictionary.exists("american"));
        assertFalse(trieDictionary.exists("america"));
    }
}

src/main/resources/words_small.txt

how
i
met
your
mother
is
an
american
sitcom
created
by
craig
thomas
and
carter
bays
for
CBS

14.02.2025